Morton Coding & Concurrency

Note:

Images show 2D grids; the same concepts apply to 3D grids.

Distance Guarantees

The foundation of a Morton-based spatial concurrency scheme is the implicit distance guarantees provided by the system. All cells for which the lowest set of bits match (2 bits for 2D , 3 for 3D) are at least 2 cells apart.

1 set

All cells for which the lowest 2 sets of bits match (4 bits for 2D , 6 for 3D) are at least 4 cells apart. All cells for which the lowest 3 sets of bits match (6 bits for 2D , 9 for 3D) are at least 8 cells apart, and so on.

2 sets (hexadecimal)

Implications for Concurrency

The distance guarantees provided by the system give us our basic concurrency principle: cells for which the lowest N sets of bits match can be processed in parallel with exclusive access to all cells within 2^(N-1)-1 of themselves.

2 sets (hexadecimal)

3 sets (hexadecimal)

It's also important to note that the distance guarantees from the lower N-1 sets are unaffected.

2 sets (hexadecimal)

3 sets (hexadecimal)

The Basic Concurrency Model

At 2 sets of bits, this gives us the basic Morton-based concurrency model:

2 sets (hexadecimal)

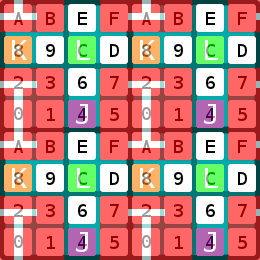
 for (uint8 i = 0; i < 0x10; ++i)
 {
     uint8 j = (i-0xC) & 0xF; //start at 0x4
     uint8 k = (i-0x8) & 0xF; //start at 0x8
     uint8 l = (i-0x4) & 0xF; //start at 0xC

     #pragma omp parallel sections default(shared)
     {
         #pragma omp section
         { //task I - 3x3 access
             #pragma omp parallel for
             for (size_t m = i; m < END; m += 0x10)
                 do_task_i(m);
         }

         #pragma omp section
         { //task J - 1x1 access
             #pragma omp parallel for
             for (size_t m = j; m < END; m += 0x10)
                 do_task_j(m);
         }

         #pragma omp section
         { //task K - 1x1 access
             #pragma omp parallel for
             for (size_t m = k; m < END; m += 0x10)
                 do_task_k(m);
         }

         #pragma omp section
         { //task L - 1x1 access
             #pragma omp parallel for
             for (size_t m = l; m < END; m += 0x10)
                 do_task_l(m);
         }
     } //end omp parallel sections
 }

Task I maintains exclusive access to 3x3 groups of cells. Tasks J, K, and L each maintain exclusive access to their respective cells, but no adjacent cells. Also, the order in which the tasks process each cell relative to other tasks is constant. L always follows I, which always follows J, which always follows K, which always follows L... The task with 3x3 access is arbitrary.

More Complex Concurrency Models

3 sets of bits gives rise to more complex concurrency models, such as a 7x7 task and 3 1x1 tasks:

3 sets (hexadecimal)

Or just as easily, a 5x5 task and 3 3x3 tasks:

3 sets (hexadecimal)

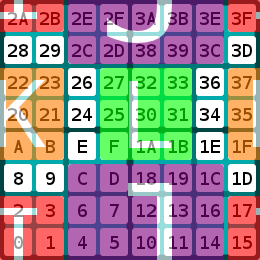
The possible configurations increase with each set of bits, but the processing code is virtually identical:

 for (uint8 i = 0; i < 0x40; ++i)
 {
     uint8 j = (i-0x30) & 0x3F; //start at 0x10
     uint8 k = (i-0x20) & 0x3F; //start at 0x20
     uint8 l = (i-0x10) & 0x3F; //start at 0x30

     #pragma omp parallel sections default(shared)
     {
         #pragma omp section
         { //task I
             #pragma omp parallel for
             for (size_t m = i; m < END; m += 0x10)
                 do_task_i(m);
         }

         #pragma omp section
         { //task J
             #pragma omp parallel for
             for (size_t m = j; m < END; m += 0x10)
                 do_task_j(m);
         }

         #pragma omp section
         { //task K
             #pragma omp parallel for
             for (size_t m = k; m < END; m += 0x10)
                 do_task_k(m);
         }

         #pragma omp section
         { //task L
             #pragma omp parallel for
             for (size_t m = l; m < END; m += 0x10)
                 do_task_l(m);
         }
     } //end omp parallel sections
 }

It's obviously possible to run 1x1 tasks in any unused cells, or devise more complex layouts not based on 4-point ordering. However, that usually requires lookup tables or more involved math to determine which cell groups are available.